Introduction
Hey there, I hope you’re doing good. In the previous blog, we discussed the meaning & types of the knapsack problem. Moreover, In this blog, you’ll get to know about solving knapsack problem using greedy method.
Let’s get started….
Knapsack Problem:
Firstly, we have given a knapsack of the maximum capacity of m kg and n items with their weight and profit. Fill in the knapsack with a subset of items such that the selected weight is less than or equal to the capacity of the knapsack and the profit of items is maximum.
Algorithm of solving Knapsack Problem using
Greedy Method:
->Assume a knapsack of capacity M and n items having profit pi and weight wi
->Sort items by profit/weight ratio: pi/wi
->Consider items in order of decreasing ratio
->Take as much of each item as possible.
->Traverse this sorted list as:
if(wi ≤ M)
{
Xi=1;
M=M-wi;
}
else if (wi > M && M>0)
{
Xi=M/wi;
M=0;
}
else
{
Xi=0;
}
Example:-
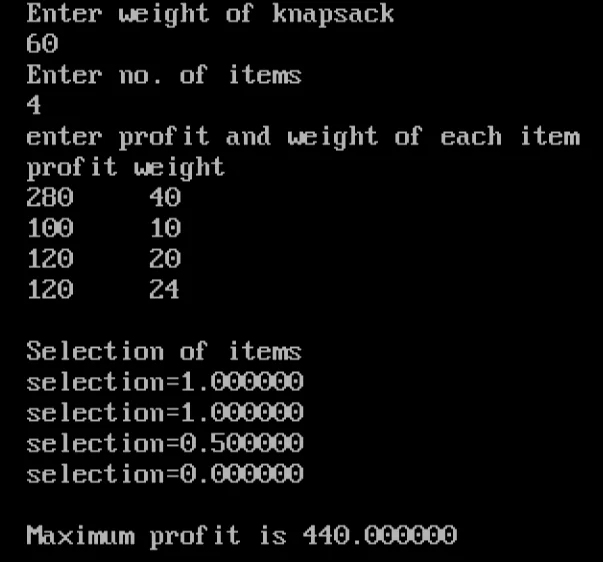
Let us consider that the capacity of the knapsack M=60 and the list of provided items are shown in the following table-
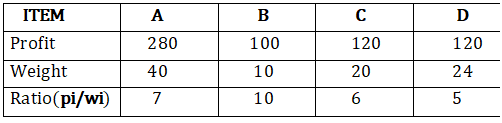
However, the provided items are not sorted based on (pi/wi). After sorting, the items are shown in the following table.
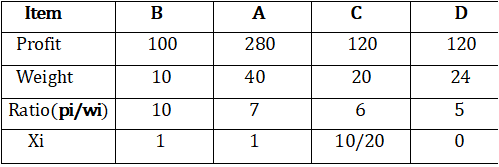
Solution:-
Afterward, sorting all the items according to (pi/wi), first item B is chosen as the weight of B is less than the capacity of the knapsack. Next, item A is chosen, as the available capacity of the knapsack is greater than the weight of A. Then, C is chosen as the next item.
However, the whole item cannot be chosen as the remaining capacity of the knapsack is less than the weight of C.
Hence, fraction of C (i.e.(60-50)/20)is chosen.
Chiefly, the capacity of the knapsack is equal to the selected items. Hence, no more items can be selected.
So, the total weight of the selected items is 10+40+20*(10/20)=60
Also, the total profit is 100+280+120*(10/20)=380+60=440
Hence, this is the optimal solution. Moreover, we cannot gain more profit by selecting any different combination of items.
Program to solve knapsack problem using greedy method:


Blog by: Mr. Rahul Agarwal
Department of Information Technology
Biyani Group of Colleges, Jaipur
Thank you
for reading the blog. Kindly, share it with the IT students as well as with the ‘tech lovers’.
CLICK HERE
to pursue Graduation courses by sitting at your home


