Introduction
Hello there, I hope you’re doing well. You’ve already read about the knapsack problem & its solution using the Greedy method. In this blog, you’ll learn to solve the 0/1 knapsack problem using dynamic programming. So, keep reading till the end of the blog for the solution.
Let’s get started…..
Knapsack problem:
Given a knapsack of maximum capacity M kg and N items with its own weight and profit. Fill in the knapsack with a subset of items such that the weight is less than or equal to the limit of the knapsack and the value of items is maximum.
0/1 Knapsack Problem:-
In this either the whole item can be selected(1) or not selected at all(0) i.e. we can select a portion of any item according to the need. We can choose not some portion of any item as and when needed.
It can be represented in the following form:
Max z=∑ni=1pi*xi
S.t.∑ni=1wi≤m
And xi=1 or 0
Where, p=profit
w=weight
x=solution or selection value
m=capacity and
s.t.=subject to
0/1 Knapsack problem using Dynamic Programming:
- In this problem, we have a Knapsack that has a capacity m.
- There are items i1,i2,….,in each having weight w1,w2,…..wn and some benefit(value or profit) associated with it p1,p2,….,pn
- Our objective is to maximize the benefit such that the total weight inside the Knapsack is at most m.
- Since this is a 0-1 Knapsack problem, we can either take an entire item or reject it completely. We cannot break an item and fill the Knapsack.
- To solve 0/1 knapsack problem using dynamic programming use the following recursive formula:-
fn(m)=max[fn-1(m);fn-1(m-wn)+pn]
fn(-m)=-∞
f0(m)=0
Example:-
Assume that we have a Knapsack with max weight capacity m=8.
Our objective is to fill the Knapsack with items such that the benefit (profit) is maximum.
The following table contains the items along with their value and weight.
| Item i | 1 | 2 | 3 |
| Profit p | 15 | 20 | 21 |
| Weight w | 5 | 4 | 3 |
Total items i.e. n=3
First apply this formula:- fn(m)=max[fn-1(m);fn-1(m-wn)+pn]
Set-1:- f3(8)=max[f2(8);f2(8-3)+21] …………………….1
f2(8)=max[f1(8);f1(4)+20] ………………………2
f2(5)=max[f1(5);f1(1)+20] ……………………….3
f1(8)=max[f0(8);f0(3)+15] ………………………..4
f1(4)=max[f0(4);f0(-1)+15] ……………………….5
f1(5)=max[f0(5);f0(0)+15] ………………………..6
f1(1)=max[f0(1);f0(-4)+15] ………………………..7
Apply:- fn(-m)=-∞
and f0(m)=0
Set-2:- f0(8)=0……………………………………8
f0(3)=0…………………………………….9
f0(4)=0……………………………………10
f0(-1)=-∞…………………………………11
f0(5)=0……………………………………12
f0(0)=0……………………………………13
f0(1)=0……………………………………14
f0(-4)=-∞…………………………………15
Set-3:- Put equation 8 to 15 into 4 to 7:-
f1(8)=max[0;0+15]=15………………………….16
f1(4)=max[0;-∞+15]=0………………………….17
f1(5)=max[0;0+15]=15………………………….18
f1(1)=max[0;-∞+15]=0………………………….19
Set-4:- Put equation 16 to 19 into 2 and 3 :-
f2(8)=max[15;0+20]=20………………………….20
f2(5)=max[15;0+20]=20………………………….21
Set-5:- Put equation 20 and 21 into 1:-
F3(8)=max[20;20+21]
max[20,41]
Maximum profit=41
Program to solve 0/1 Knapsack problem using dynamic programming:-
#include<stdio.h>
#include<conio.h>
int max(int a,int b){return(a>b)?a:b;}
int KnapSack(int W,int wt[],int val[],int n)
{
int i,w;
int K[20][20];
for(i=0;i<=n;i++)
{
for(w=0;w<=W;w++)
{
if(i==0||w==0)
K[i][w]=0;
else if(wt[i-1]<=w)
K[i][w]=max(val[i-1]+K[i-1][w-wt[i-1]],K[i-1][w]);
else
K[i][w]=K[i-1][w];
}
}
return K[n][W];
}
void main()
{
int i,n,val[20],wt[20],W;
clrscr();
printf(“Enter number of items:”);
scanf(“%d”,&n);
printf(“Enter value and weight of items:\n”);
for(i=0;i<n;++i)
{ scanf(“%d%d”,&val[i],&wt[i]);
}
printf(“Enter size of Knapsack:”);
scanf(“%d”,&W);
printf(“%d”,KnapSack(W,wt,val,n));
getch();
}
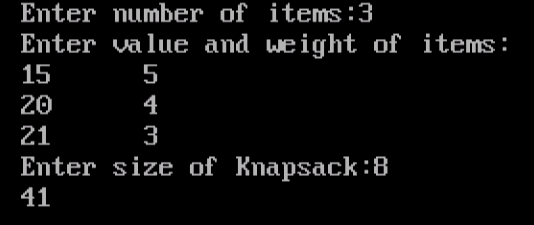
Output:-
Blog By:- Mr. Rahul Agarwal (Assistant Professor)
Department Of Information Technology
Biyani Group Of Colleges, Jaipur
CLICK HERE
to pursue your Graduation by sitting at your home.